Damped Natural Frequency
A circuit containing resistance (R), capacitive (C) reactance and inductive (L) reactance components will offer an impedance to an applied AC waveform that depends on the waveform’s frequency – but not linearly. Instead, the capacitive reactance diminishes with increasing frequency, while the inductive reactance increases. As these reactances are out of phase with one another, every LCR circuit has a frequency for which the two reactances exactly cancel one another out; the circuit’s impedance at that frequency is at its minimum, comprising only its resistance.
The frequency at which this occurs for a particular circuit is known as its resonant or natural frequency, and can be calculated from the relationship
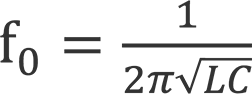
where f0 is resonant frequency in Hertz, L is the circuit’s inductance in Henrys and C is its capacitance in Farads.
An ideal LC circuit could oscillate at this frequency for an infinite duration without any externally applied waveform, by passing energy back and forth between the capacitor’s electrical field and the inductor’s magnetic field. However, circuits with only inductive and capacitive reactances do not exist in reality; an amount of resistance is always present as well. This will act to damp out the oscillations, which will eventually die away entirely. Their electrical energy is dissipated as heat energy in the circuit’s resistance.
Circuits like this are known as harmonic oscillators, and they are analogous to mechanical systems with a pendulum swinging back and forth. The circuit’s resistance equates to friction in the pendulum’s bearings.